Đường tròn nội tiếp tam giác là gì? Tính chất và cách xác định nội
Nhằm giúp các bạn học sinh Trung học Phổ thông nắm vững nội dung kiến thức về đường tròn – đường tròn nội tiếp tam giác, ở bài viết dưới đây Bamboo school sẽ cung cấp chi tiết các khái niệm, tính chất cũng như là cách xác định đường tròn nội tiếp. Hy vọng với bài viết này sẽ giúp các bạn học sinh của chúng ta nắm chắc nền tảng kiến thức về đường tròn – đường tròn nội tiếp.
Đường tròn là gì? Đường tròn nội tiếp tam giác là gì?
Khái niệm đường tròn
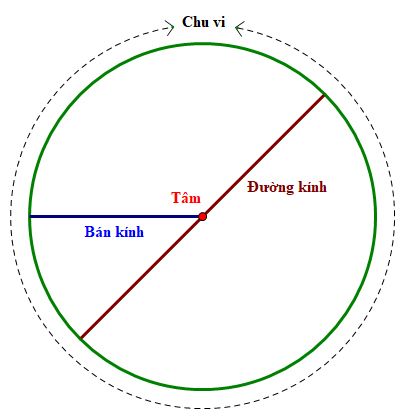
Đường tròn (hoặc vòng tròn) là tập hợp của tất cả những điểm trên một mặt phẳng, cách đều một điểm cho trước bằng một khoảng cách nào đó. Điểm cho trước gọi là tâm của đường tròn, còn khoảng cho trước gọi là bán kính của đường tròn.
Đường tròn có tâm O và bán kính r được ký hiệu là (O;r)
Khái niệm đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác đó (hay ta còn nói tam giác ngoại tiếp đường tròn)
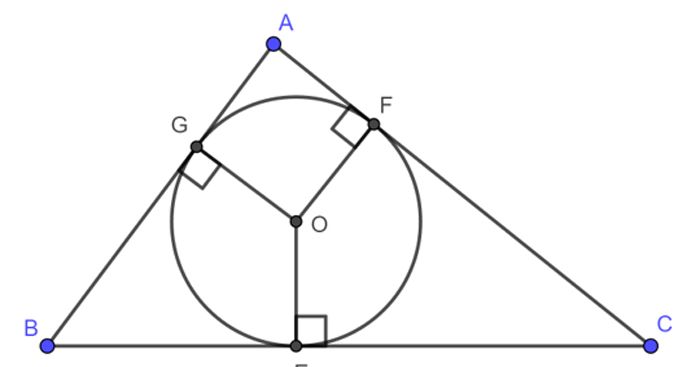
Nói một cách đơn giản hơn, đường tròn nội tiếp của một tam giác là đường tròn nhỏ nhất nằm trong tam giác; nó tiếp xúc với cả ba cạnh của tam giác. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong.
Tính chất đường tròn nội tiếp tam giác
- Mỗi một tam giác chỉ có duy nhất 1 đường tròn nội tiếp.
- Tâm của đường tròn nội tiếp tam giác là giao điểm giữa 3 đường phân giác của tam giác đó do đó bán kính của đường tròn nội tiếp tam giác chính bằng khoảng cách từ tâm hạ vuông góc xuống ba cạnh của tam giác.
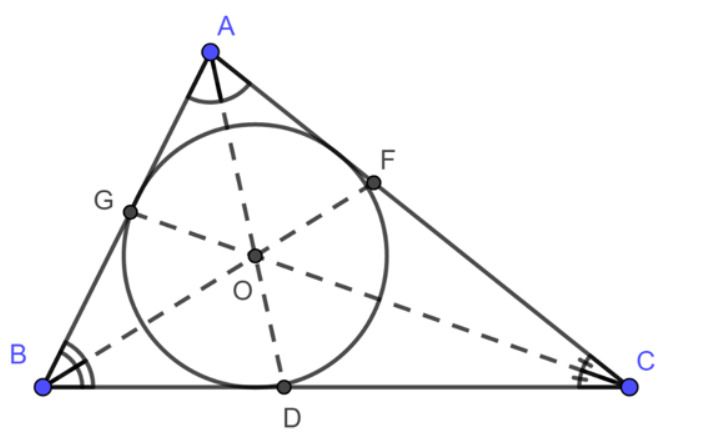
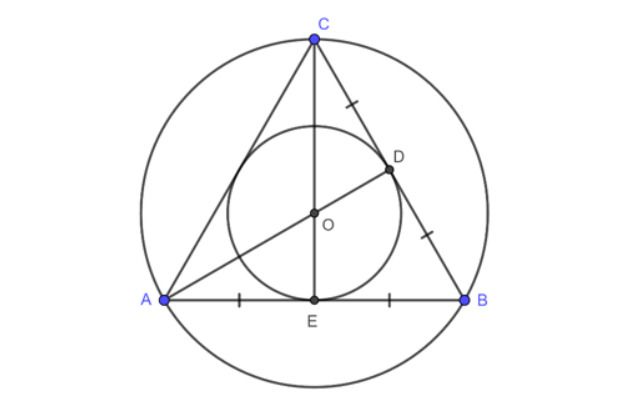
Ví dụ: Quan sát và phân tích hình vẽ trên ta có:
- ΔABC có 3 đường phân giác lần lượt là AD, BF, CG ⇒ Giao điểm của 3 đường phân giác chính là tâm O của đường tròn.
- Vẽ đường tròn tâm O với lần lượt các bán kính OD = OF = OG = r
- Đối với tam giác đều, đường tròn ngoại tiếp và nội tiếp tam giác có cùng tâm đường tròn với nhau.
Cách xác định đường tròn nội tiếp
Để xác định được vị trí của đường tròn nội tiếp tam giác, ta cần phải ghi nhớ thật kỹ lý thuyết:
“Tâm đường tròn nội tiếp của tam giác là giao điểm của ba đường phân giác trong của tam giác đó (có thể là 2 đường phân giác)”
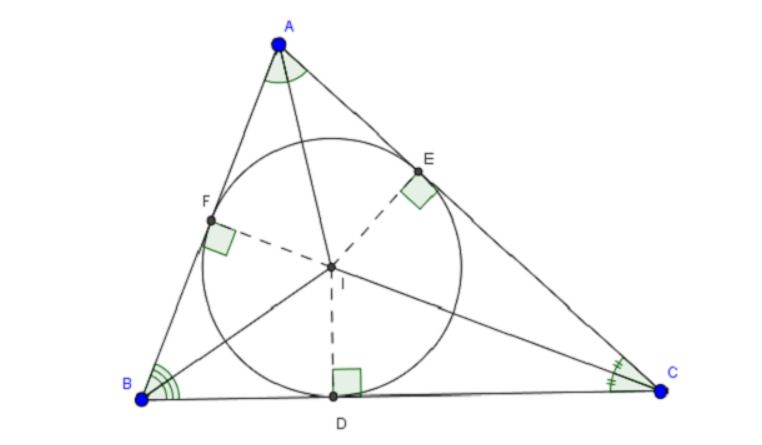
Ví dụ. Cho ΔABC, tiến hành xác định vị trí của tâm I đường tròn nội tiếp ΔABC. Ta có các bước sau đây:
- Vẽ 3 đường phân giác trong của ΔABC (có thể vẽ 2 đường phân giác). 3 đường phân giác lần lượt được gọi là AD, BE, CF.
- Xác định giao điểm I của 3 đường phân giác trong ΔABC.
- Từ tâm I, lần lượt kẻ 3 đường vuông góc với 3 cạnh AB, AC, BC của ΔABC. 3 đường vuông góc này chính là bán kính của đường tròn tâm I.
- Tiến hình vẽ đường tròn tâm I với bán kinh r = IF = IE = ID (như hình vẽ)
Các trường hợp đường tròn nội tiếp
Đường tròn nội tiếp có thể xảy ra với tất cả các loại tam giác: tam giác vuông, tam giác tù, tam giác nhọn.
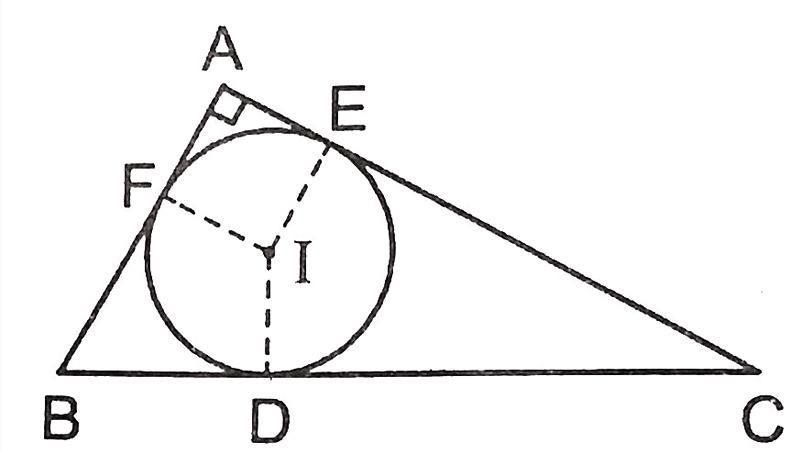
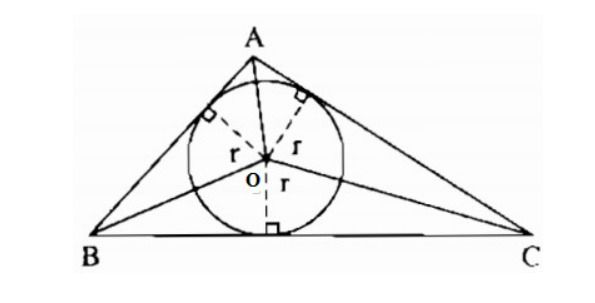
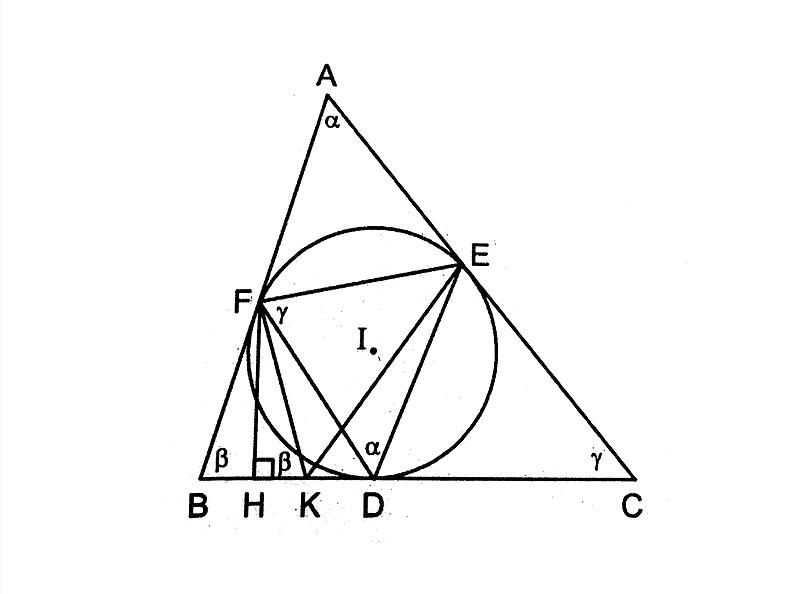
Đặc biệt, trong trường hợp nếu tam giác đó là tam giác đều thì đường tròn ngoại tiếp và nội tiếp tam giác có cùng tâm đường tròn với nhau.
Xem thêm:
- Trực tâm là gì? Tính chất và cách xác định trực tâm trong tam giác
- Công thức tính diện tích tam giác, hình thoi, hình vuông, hình chữ nhật, hình tròn
- Công thức tính chu vi hình vuông, chữ nhật, tam giác, hình tròn, hình thoi
Trên đây là tổng hợp khái niệm và những tính chất cơ bản của hình tròn nội tiếp tam giác. Hy vọng bài viết có thể giúp cho các bạn có thể hiểu rõ hơn về khái niệm này. Qua đó, có được sự chuẩn bị tốt nhất cho những bài học sắp tới.
Theo dõi chúng tôi www.hql-neu.edu.vn để có thêm nhiều thông tin bổ ích nhé!!!
![[SGK Scan] Bài 7. Sóng cơ và sự truyền sóng cơ – Sách Giáo Khoa](https://i.ytimg.com/vi/qIOKuLx7h-4/mqdefault.jpg)